Unsupervised Learning

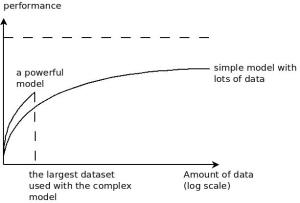
Deep neural networks have enjoyed a fair bit of success in speech recognition and computer vision.  The same basic approach was used for both problems:  use supervised learning with a large number of labelled examples to train a big, deep network to solve the problem.   This approach just works whenever the solution to the problem that we seek to solve can be represented with a deep neural network, which is often the case for reasons that I will not explain here.

But there is another way.  Unsupervised learning is the idea that we can understand how the world “works” by simply passively observing it and building a rich internal mental model of it.  This way, when we have a supervised learning task we wish to solve, we can consult the mental model that was learned during the unsupervised learning stage, and solve the problem much more rapidly, without using as many labels.   Unsupervised learning is very appealing, because it doesn’t require any labels.  Imagine:  you simply get a system to observe the world for a while, and after a while we could use it to answer difficult questions about the signal — such as to determine what objects are in an image, what are their 3D shapes, and and what are their poses.

But so far there are no state of the art results that benefit use unsupervised learning.   Why?

1:  We don’t have the right unsupervised learning algorithm:  Supervised learning algorithms work well because they directly optimize the performance measure that we care about and come with a guarantee:  if the neural network is big enough and is trained on enough labelled data, the problem will be completely and utterly solved.  In contrast, unsupervised learning algorithms do not have such a guarantee.   Even if we used the best current unsupervised learning algorithm, and trained it on a huge neural net with a huge amount of data, we could not be confident that it would help us build high-performing systems.

2: Whatever the unsupervised learning algorithm will do, it will necessarily be different from the objective that we care about. As the unsupervised learning algorithm doesn’t know about what the desired objective is, the only thing it can do is to try and understand as much of the signal as possible, in order to, hopefully, understand the relevant bits about the problem we care about.  Thus, if it takes a big network to do really well the purely supervised problem (as is the case —- the high-performing supervised nets have 50M parameters, and they’re still growing), where all the network’s resources are dedicated to the task, it will take a much larger network to really benefit from unsupervised learning, since it attempts to solve a much harder problem that includes our supervised objective as a special case.

Thus, at this point, it is simply not clear how and why will the future unsupervised learning algorithms work.

Universal Approximation and Depth

Many years ago Hornik et al. proved that a neural network with a single hidden layer can approximate any continuous function from a compact domain to the reals to arbitrary precision. The paper is highly cited (search for “Multilayer feedforward networks are universal approximators” on google scholar; this paper has almost almost 1/3 of the citations of the original backpropagation paper!), and convinced many people that neural networks will work for their applications, as they can learn any function.

Sadly this result was very misleading. The result claimed that a single hidden layer neural network can approximate any function, so a one hidden layer neural network should be good for any application. However it is not an efficient approximator for the functions we care about (this claim is true but hard to defend, since it’s not so easy to describe the functions that we care about). Indeed, the universal approximation construction works by allocating a neuron to every to every small volume of the input space, and learning the correct answer for each such volume.  The problem is that the number of such small volumes grows exponentially in the dimensionality of the input space, so Hornik’s construction is exponentially inefficient and is thus not useful.  (it is worth noting that deep neural networks are not universal approximators unless they are also exponentially large, because there are many more different functions than there are small neural networks).

This caused researchers to miss out on the best feature of the neural networks: depth. By being deep, the neural network can represent functions that are computed with several steps of computation.  Deep neural networks are best thought of as constant-depth threshold circuits, and these are known to be able to compute a lot of interesting functions.  For example, a small 3-hidden layer threshold network can sort N N-bit numbers, add N such numbers, compute their product, their max,  compute any analytic function to high precision.  And it is this ability of deep neural networks to perform such interesting computations makes them useful for speech recognition and machine translation.

There is another simple reason why large but not infeasibly huge deep networks must be capable of doing well on vision and speech.  The argument is simple:  human beings can recognize an object in 100 milliseconds, which gives their neurons the opportunity to fire only 10 times during the recognition.  So there exists a parallel procedure that can recognize an object in 10 parallel steps, which means that a big 10-layer net should be good at vision and speech — and it turns out to be the case.    But if this argument is actually valid, it means that we should be able to train neural networks for any task that humans can solve quickly.  Reading emotions, recognizing faces, reading body language and vocal intonation, and some aspects of motor control come to mind.  On all these tasks, high performance is truly achievable if we have the right dataset and fast implementation of a big supervised network.

In addition, there is a well-known intuition for why deep convolutional neural networks work well for vision, and explain why shallow neural networks do not. Many believe that to recognize an object, many steps of computation should be performed. In the first step, the edges should be extracted from the image. In the second step, small parts (or edges of edges) should be computed from the edges, such as corners. In the third step, combinations of small parts should be computed from the small parts. They could be a small circle, a t-junction, or some other visual entity. The idea is to extract progressively more abstract and specific units at each step. If you found this description difficult to follow, here are some images of various object recognition systems, all of which work roughly on the principle of extracting larger parts from smaller ones.

 (from http://www.kip.uni-heidelberg.de/cms/vision/projects/recent_projects/hardware_perceptron_systems/image_recognition_with_hardware_neural_networks/)

(from http://www.sciencedirect.com/science/article/pii/S0031320308004603)

(from http://journal.mercubuana.ac.id/data/Hierarchical-models-of-object-recognition-in-cortex.pdf)

By being deep, the convolutional neural network can implement this multistep process. The depth of the convolutional neural network allows each of its layers to compute larger and more elaborate object parts, so that the deepest layers compute specific objects. And its large number of parameters and units allows it to do so robustly, provided that we manage to find the appropriate network parameters.

Something similar must be going on with speech recognition, where deep networks make a very big difference compared to shallow ones, so it is likely that speech recognition consists of breaking speech up into small “parts”, and increasing their complexity at each layer, which cannot be done with a shallow network.

Calling Python from Matlab

It is sometimes useful to call Python from Matlab. There may be a robust implementation of an optimizer that hasn’t been well-ported to Python yet. What to do in this situation?

There is a simple strategy that should do: first, figure out how to call python from stand-alone C functions, and then use that code within a mex function. While tedious, at least this is straightforward. By using the not terribly complicated PyObject stuff we can create python objects in C, send them to python functions, and unpack whatever the python functions give us back.

However, everything goes bad if we try to import numpy in our python code. We’ll get an error that looks like this:
……../pylib/numpy/core/multiarray.so:
undefined symbol: _Py_ZeroStruct
even though all the required symbols are defined in libpython2.x.

This problem was asked several times on stackoverflow, with no satisfactory answer. But luckily, after much searching, I stumbled upon https://github.com/pv/pythoncall which discovered a way to solve this problem.

Basically, matlab imports dynamic libraries in a peculiar way that messes up the symbols somehow. But if we execute the code

int dlopen_python_hack(){
if (!dlopen_hacked){
printf(“Preloading the library for the hack: %s\n”, LIBPYTHON_PATH);
dlopen(LIBPYTHON_PATH, RTLD_NOW|RTLD_GLOBAL);
dlopen_hacked = 1;
}
}

where LIBPYTHON_PATH points to libpython2.x.so, then suddenly all the messed-up symbols will fix themselves, and we won’t have undefined symbol problems anymore.

The useless beauty of Reinforce

Reinforce is one of my favorite algorithms in machine learning. It’s useful for reinforcement learning.

The formal goal of reinforce is to maximize an expectation, , where is the reward function and is a distribution. To apply reinforce, all we need is to be able to sample from and to evaluate the reward , which is really nothing.

This is the case because of the following simple bit of math:

which clearly shows that to estimate the gradient wrt the expected reward, we merely need to sample from and weigh the gradient by the reward .

Reinforce is so tantalizing because sampling from a distribution is very easy. For example, the distribution could be the combination of a parametrized control policy and the actual responses of the real world to our actions: could be the sequence of states and actions chosen by our policy and the environment, so

,

and only part of is parameterized by .

Similarly, is obviously easily computable from the environment.

So reinforce is dead easy to apply: for example, it could be applied to a robot’s policy. To sample from our distribution, we’d run the policy, get the robot to interact with our world, and collect our reward. And we’ll get an unbiased estimate of the gradient, and presto: we’d be doing stochastic gradient descent on the policy’s parameters.

Unfortunately, this simple approach is not so easy to apply. The problem lies in the huge variance of our estimator . It is easy to see, intuitively, where this variance comes from. Reinforce obtains its learning signal from the noise in its policy distribution . In effect, reinforce makes a large number of random choices through the randomness in its policy distribution, and if they do better than average, then we’ll change our parameters so that these choices are more likely in the future. Similarly, if the random choices end up doing worse than random, the model will try to avoid choosing this specific configuration of actions.

( = because . There is a simple formula for choosing the optimal ).

To paraphrase, reinforce adds a small perturbation to the choices and sees if the total reward has improved. If we’re trying to do something akin to supervised learning with reinforce with a small label set, then reinforce won’t do so terribly: each action would be a classification, and we’d have a decent chance to guess the correct answer. So we’ll be guessing the correct answer quite often, which will supply our neural net with training signal, and learning will succeed.

However, it’s completely hopeless to train a system that makes a large number of decisions with a tiny reward in the end.

On a more optimistic note, large companies that deploy millions of robots could refine their robot’s policies with large scale reinforce. During the day, the robots will collect the data for the policy, and during the night, the policy will be updated.

Undirected models are better at sampling

The best directed models should always be a worse at generating samples than the best undirected models, even if their log likelihoods are similar for a simple reason.

If we have an undirected model, then it defines a probability distribution by the equation

As always, the standard objective of unsupervised learning is to find a distribution so that the average log probability of the data distribution is as large as possible.

In theory, if we learn successfully, we should reach a local maxima of the average log probability. Taking the derivative and setting it to zero yields

(here are the maximum likelihood parameters). Notice that this equation is a statement about the samples produced by the distribution : the gradient of the goodness averaged over the data distribution is equal to the same gradient averaged over the model’s distribution .  Therefore, the samples from must somehow be related to the samples from the data distribution . This is a “promise” made to us by the learning objective of unsupervised learning.

However, directed models do not offer such a guarantee; instead, it promises that the conditional distributions of the data distribution will be similar to the conditional distributions of the model’s distribution, when the conditioned data is sampled form the data distribution. This is the critical point.

More formally, a directed model defines a distribution . Plugging it in into the objective of maximizing the average log likelihood of the data distribution , we get the following:

,

which is a sum of indepedent problems.

IF the ‘s don’t share parameters for different ‘s, then the problems are truly independent and could be solved completely separately. So let’s say we found a that makes all these objectives happy. Then will be happy, which means that is similar, more or less, to for being sampled from — which is the critical implied assumption made by the maximum likelihood objective applied to directed models. Why is it a problem when generating samples? It’s bad because this objective makes no “promises” about the behaviour of when . It is easy to imagine that a will be somewhat different from , and say that was sampled from . Then will freak out, having never seen anything like , which will make the sample look even less like a sample from . Etc. This “chain reaction” will likely cause the directed model to produce worse-looking samples than an undirected model with a similar log probability.

But something should be odd: after all, any undirected model (or distribution for that matter) can be decomposed with the chain rule, . Why won’t the above argument apply to an undirected model, which I claim is to be superior at sampling? An answer can be given, but it involves lots of handwaving.

If an undirected model is expressed as a directed model using the chain rule, then the conditional probabilities will involve massive marginalizations. What’s more, all the conditional distributions will share parameters in a very complicated way for different values of . In all likelihood (and that’s the weak part of the argument),  the parameterization is so complex that it’s not possible to make all the objectives   happy for all simultaneously; that is, the undirected model will not necessarily make similar to when . This is why I assumed that the little conditionals don’t share parameters.

So to summarize, directed models are worse at sampling because of the sequential nature of their sampling procedure. By sampling in sequence, the directed model is “fed” data which is unlike the training distribution, causing it to freak out. In contrast, sampling from undirected models requires an expensive Markov chain, which ensures the “self-consistency” of the sample. And intuitively, since we invest more work into obtaining the sample, it must be better.

The Miracle of the Boltzmann Machine

The Boltzmann Machine, invented by my adviser, is fairly well-known in machine learning. But the Boltzmann Machine (BM) is also the only model that actually uses dreams for a specific computational purpose, as opposed to all other models of sleep, that use it in a more ad-hoc way (e.g., to “remember the day’s events better”, or to “forget unwanted thoughts”, and other claims of this kind). In addition, the BM also forgets its dreams. Just like humans! The BM forgets its dreams due to a differentiation of a simple equation that has apparently nothing to do with sleep. It is so remarkable that I believe the Boltzmann Machine to be “right” in a very essential way.

Unfortunately the Boltzmann Machine can only be understood by using Math. So you’ll like it if you know math too.

The Boltzmann Machine defines a probability distribution over the set of possible visible binary vectors and hidden binary vectors . The intended analogy is that is an observation, say the pixels on the retina, and is the joint activity of all the neurons inside the brain. We’ll also denote the concatenation of and by , so . The Boltzmann Machine defines a probability distribution over the configurations by the equation

So different choices of the matrix yield different distributions .

The BM makes observations about the world, which are summarized by the world distribution over the visible vectors . For example, could be the distribution of all the images we’ve seen during the day (so is a binary image).

The following point is a little hard to justify. We define the goal of learning by the objective function

,

where and . In other words, the goal of learning is to find a BM that assigns high log probability to the kind of data we typically observe in the world. This learning rule makes some intuitive sense, because negative log probability can be interpreted as a measure of surprise. So if our BM isn’t surprised by the real world, then it must be doing something sensible. It is hard to fully justify this learnnig objective, because a BM that’s not surprised by the world isn’t obviously useful for other tasks. But we’ll just accept this assumption and see where it leads us.

So we want to find the parameter setting of that maximizes the objective , which is something we can approach with gradient ascent: we’d iteratively compute the gradient , and change slightly in the direction of the gradient. In other words, if we change our weights by

,

then we’re guaranteed to increase the value of the objective slightly. Do it enough times and our objective will be in a good place. And finally, here is the promised math:

.

If you’re into differentiation you could verify the above yourself (remember that , and similarly for ) .

We’re finally ready for the magical interpretation of the above equation. The equation states that the weight should change according to the difference of two averages: the average of the products according to and according to .

But first, notice that is the product of the two neurons at the ends of the connection . So the connection will have little trouble detecting when the product is equal to 1 from local information (remember, our vectors live in ).

More significantly, we can compute the expectation by taking the observed data from , “clamping” it onto the visible units , and “running” the BM’s neurons until their states converge to equilibrium. All these terms can be made precise in a technical sense. But the important analogy here is that during the day, the world sets the visible vectors of the BM, and it does the rest, running its hidden units until they essentially converge. Then the BM can compute the expectation by simply averaging the products that it observes. This part of the learning rule attempts to make the day’s patterns more likely.

Now is computed by disconnecting the visible vector from the world and running the BM freely, until the states converge. This is very much like dreaming; we ask the BM to produce the patterns it truly believes in. Then the connection computes its expectation by observing the products , and subtracts the resulting average from the connections. In other words, the learning rule says, “make whatever patterns we observe during sleep less likely”. As a result, the BM will not be able to easily reproduce the patterns it observed during the sleep, because it unlearned them. To paraphrase: the BM forgets its dreams.

Consequently, the BM keep on changing its weights as long as the day’s patterns are different from the sleep’s patterns, and will stop learning once they two become equal. This means that the goal of learning is to make the dreams as similar as possible to the actual patterns that are observed in reality.

It should be surprising that both dreams and the fact that they are hard to remember are a simple consequence of a simple equation.

The futility of gigantic training sets with simple models

It is believed that a simple, usually linear, model with an extra-huge training set and a gigantic feature representation is superior to a more powerful model with less data, a claim often made by Google. And indeed, large companies are able to get better results by using ever larger training sets with simple models: each order of magnitude increase in the training set results in a reasonable increase in performance.

This approach is sensible in the sense that increasing the size of the training data is essentially guaranteed to improve performance. And if I have a fast learning algorithm, thousands of cores, and lots of data, then it is conceptually trivial to use more training data whenever the learning algorithm can be parallelized without too much engineering effort. And if I needed better performance very soon, I’d do precisely that.

However, the problem with this approach is that it runs out of steam in the sense that it will not reach human level performance. The following figure illustrates the point:

In this figure, the simpler model eventually outperforms the more sophisticated one, mainly because it is easy and relatively cheap to make the model larger. However, simple models will necessarily fail to reach human level performance, and the more powerful models will eventually but certainly outperform them. It must be so, hence QED. More seriously, a model could not successfully solve tasks that involve any kind of text comprehension, for example, without first extracting a really good representation of text’s meaning with miraculous-looking properties. And that’s something simple models don’t even try to do. By not using a good representation, the simple model falls back on its more primitive feature representation, which does explicitly describe the higher-level concepts that are ultimately needed to solve our task.

Nonetheless, simple (ie linear) models have serious advantages over complex models. They are faster to train and are easier to extend and understand, and their behaviour and performance is more predictable. However, it is finally becoming recognized that neural networks have the potential to be vastly more expressive than linear models without using too many parameters. And now that we are becoming better at trainign deep neural networks, we will see the proliferation of the more powerful multilayered perceptrons. Of course, naive multilayered perceptrons will also probably run out of steam, in which case we’ll have to design more exotic and ambitious architectures. But for now they are the simplest and the most powerful model class.

Validation Error Shape

Most learning algorithms make many small changes to the model, ensuring that each little change improves the model’s fit of the training data.  But when the model starts getting too good at the training data, its test and validation error get worse. That’s the point where we stop learning because additional learning will improve improve our training error at the expense of the validation and the test error.

Many machine learning courses depict a cartoon of the validation error:

Note that both the training and the validation errors are convex functions of time (if we ignore the bit in the beginning). However, if we train the model longer, we discover the following picture:

This is the real shape of the validation error. The error is almost always bounded from above, so the validation error must eventually inflect and converge. So the training error curve is convex, but the validation isn’t!